Have you ever wondered how trigonometric identities were created? Trigonometry is a fascinating branch of mathematics that can be applied to many different fields. What are the most important trigonometric identities to memorize?
In this blog, we will discuss the history and development of trigonometric identities, as well as what they are used for.
How Were The Trigonometric Identities Created?
The trigonometric identities are a set of equations that express basic trigonometry ratios in terms of one another. The trigonometric identities are an important part of solving trigonometry problems and are often used to reduce the complexity in trigonometric calculations. Trig identities are also useful for simplifying expressions involving trig functions.
The history of trigonometry starts with the study of triangles where angles were measured using degrees. It was later discovered that there could also be angles measured in radians from 0° up to 360°. A revolution occurred when mathematicians realized they could calculate sines, tangents, and other trigonometric functions using the same set of trigonometric identities.
There are many different relationships that can be derived from these basic trigonometric equations but they all share a common technique: reduce complex multiplication and division to addition and subtraction, respectively.
What Are The Most Important Trigonometric Identities To Memorize?
The only ones that are absolutely necessary to memorize are the ones with long derivations, like the sum and difference formulas for sine and cosine or the half-angle formulas. However, learning most of them will improve speed and efficiency on most problems.
Important trigonometric identities to memorize are the long derivations, which include the sum and difference formulas for sine and cosine or the half-angle formulas.
Learning most of them (especially the reciprocal) will improve speed on solving most problems, but that’s not absolutely necessary (since you can always access them here).
Reciprocal (Definition) Identities:
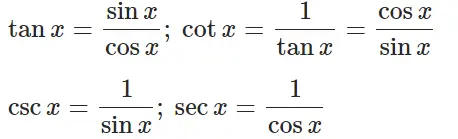
Pythagorean Identities:
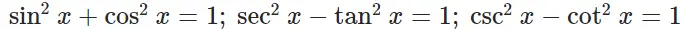
Parity Identities:
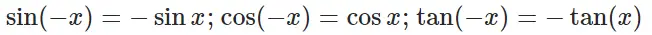
Cofunction Identities:
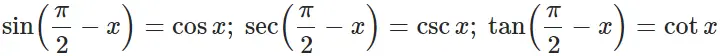
Addition/Subtraction Formulas:
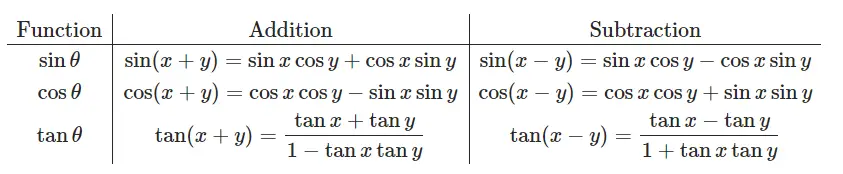
Double/Half Angle Formulas:
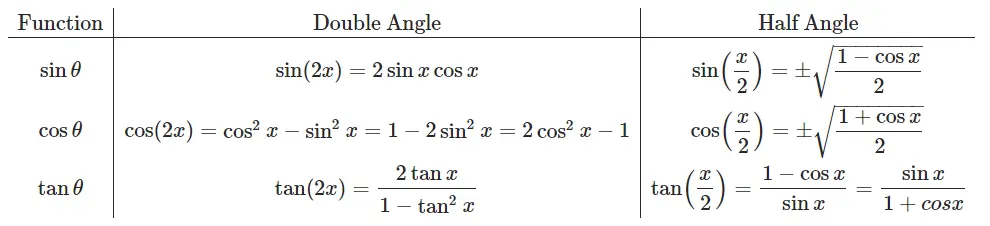
Power Reduction Formulas:
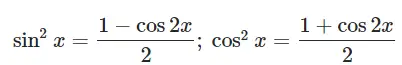
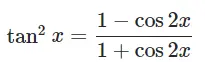
Can I Get A Trigonometry Formulas List?
Here are 2 important trigonometry sheets with a list of important formulas that we’ve found most useful:





